If you’ve ever found yourself drowning in a sea of inefficient code, you’re not alone. Understanding and mastering time and space complexity can feel like trying to learn a new language. But fear not! We’re here to guide you through the labyrinth of these essential programming concepts with some humor and a bit of fun. By the end of this article, you’ll have a solid grasp of how to optimize your code, and maybe even impress your colleagues with your newfound knowledge.
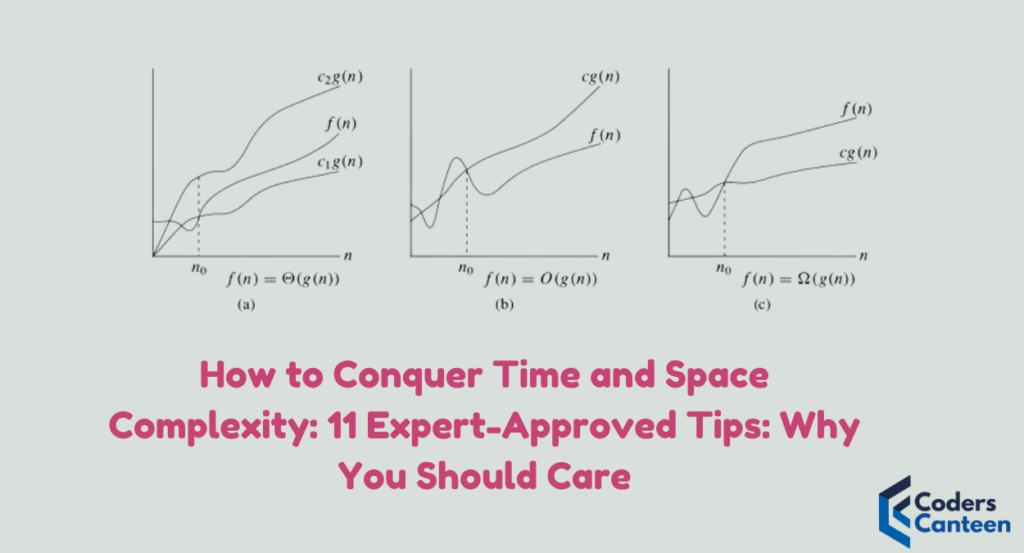
1. Know Your Big O Notation
Big O notation is like the secret code for understanding how your algorithms perform. It’s a way to describe the efficiency of an algorithm in terms of time (how long it takes to run) and space (how much memory it uses). Think of it as the Yelp review for your code.
- O(1) – Constant Time: The holy grail of efficiency. No matter how big your data set, it takes the same amount of time to complete.
- O(n) – Linear Time: The time it takes grows proportionally with the size of the input.
- O(n^2) – Quadratic Time: The time it takes is proportional to the square of the input size. Avoid this like you avoid spoilers for your favorite TV show.
- O(log n) – Logarithmic Time: Grows slower than the size of the input. Great for large data sets.
- O(n log n) – Linearithmic Time: A combination of linear and logarithmic. Efficient for many sorting algorithms.
Funny Line: Think of Big O notation as the “what’s the worst that could happen” guide for your code.
2. Choose the Right Data Structures
Selecting the appropriate data structure can make a huge difference in your algorithm’s performance. Lists, arrays, hash tables, trees – each has its strengths and weaknesses.
- Arrays and Lists: Great for indexed access. Not so great for insertion and deletion in the middle.
- Hash Tables: Super fast lookups (O(1)), but can be memory hogs.
- Trees: Balanced trees like AVL and Red-Black trees offer good performance for insertions, deletions, and lookups (O(log n)).
Funny Line: Choosing the right data structure is like choosing the right tool for assembling IKEA furniture. Use the wrong one, and you’ll end up with a wobbly bookshelf.
3. Master Recursion
Recursion can be both a blessing and a curse. It’s elegant and often simplifies code, but it can also lead to performance issues if not handled carefully.
- Base Case: Always ensure your recursion has a base case to avoid infinite loops.
- Tail Recursion: Try to use tail recursion where possible to optimize memory usage.
- Memoization: Store results of expensive function calls and reuse them when the same inputs occur again.
Funny Line: Recursion is like a Russian nesting doll – beautiful and intricate, but sometimes you wish it would just stop after the first few layers.
4. Optimize Loops
Loops are at the heart of many algorithms, and optimizing them can lead to significant performance gains.
- Avoid Nested Loops: Each additional nested loop can exponentially increase your algorithm’s complexity.
- Use Efficient Iteration: Prefer iterators and generators in languages like Python for better performance.
- Break Early: If you can determine an early exit condition in a loop, use it to save unnecessary iterations.
Funny Line: Nested loops are like those never-ending nested Russian dolls – entertaining at first, but eventually you just want to scream.
5. Divide and Conquer
The divide and conquer strategy involves breaking a problem down into smaller, more manageable pieces, solving each piece, and then combining the results.
- Merge Sort and Quick Sort: Classic examples of divide and conquer algorithms that are highly efficient.
- Binary Search: Another divide and conquer strategy that excels with sorted data.
Funny Line: Divide and conquer is like dealing with your laundry – break it into smaller loads, and it’s suddenly manageable (and you might actually find matching socks).
6. Dynamic Programming
Dynamic programming is a technique for solving problems by breaking them down into simpler subproblems and storing the results of these subproblems to avoid redundant calculations.
- Memoization: Store results of subproblems to save time on re-computation.
- Bottom-Up Approach: Solve smaller subproblems first and use their results to build up solutions to larger problems.
Funny Line: Dynamic programming is like cooking with leftovers – reuse, recycle, and your dinner (algorithm) is ready in no time!
7. Use Space Wisely
Just like in real life, space in programming is a valuable resource. Efficient use of space can drastically improve your algorithm’s performance.
- In-Place Algorithms: Modify the input data structure itself rather than creating a new one.
- Garbage Collection: Be aware of how your language handles memory allocation and deallocation.
Funny Line: Think of space optimization like packing for a vacation – bring only what you need, and leave those “just in case” items behind.
8. Parallel Processing
Parallel processing can significantly speed up algorithms by dividing tasks into smaller chunks and processing them simultaneously.
- Multi-threading: Use threads to run multiple parts of a program simultaneously.
- MapReduce: A programming model for processing large data sets with a distributed algorithm.
Funny Line: Parallel processing is like having multiple hands at a buffet – you can grab more food (data) faster, but don’t get greedy!
9. Profiling and Benchmarking
Profiling helps you understand where your code spends most of its time, allowing you to focus your optimization efforts where they matter most.
- Profilers: Tools like gprof, Valgrind, or built-in language profilers help identify bottlenecks.
- Benchmarking: Measure the performance of different algorithms and implementations to find the most efficient one.
Funny Line: Profiling your code is like spying on your teenage kids – you find out exactly where they (and your program) spend all their time.
Must Read:
- Data Models in DBMS: 10 Incredible Benefits of Understanding
- How to Enable Remote Desktop Access: Best 7 Command Tools
10. Learn From the Best
Studying well-known algorithms and data structures is invaluable. They are often optimized by some of the brightest minds in computer science.
- Sorting Algorithms: Learn how algorithms like Quick Sort, Merge Sort, and Heap Sort work.
- Graph Algorithms: Understand Dijkstra’s, A*, and Floyd-Warshall algorithms for shortest path problems.
Funny Line: Learning from the best is like getting cooking tips from Gordon Ramsay – your dish (algorithm) will turn out way better than you expected.
11. Practice, Practice, Practice
Finally, the best way to master time and space complexity is through practice. Solve problems, write code, and review your solutions.
- Coding Challenges: Participate in coding competitions and online platforms like LeetCode, HackerRank, and CodeChef.
- Peer Reviews: Get feedback from peers to identify areas of improvement.
Funny Line: Practicing coding is like playing an instrument – the more you do it, the less you’ll sound like a dying cat.
FAQs About Time and Space Complexity
Q: Why should I care about time and space complexity?
A: Understanding time and space complexity helps you write efficient code, which runs faster and uses fewer resources. This is especially important in large-scale applications where performance is critical.
Q: What is the difference between time complexity and space complexity?
A: Time complexity refers to the amount of time an algorithm takes to complete as a function of the input size, while space complexity refers to the amount of memory an algorithm uses relative to the input size.
Q: How can I reduce the time complexity of my code?
A: You can reduce time complexity by optimizing your algorithms, using efficient data structures, avoiding nested loops, and applying techniques like divide and conquer or dynamic programming.
Q: What are some common mistakes in handling time and space complexity?
A: Common mistakes include using inappropriate data structures, not considering edge cases, inefficient looping, and ignoring the impact of recursive calls on memory.
Conclusion
Conquering time and space complexity might seem daunting, but with these 11 expert-approved tips, you’ll be well on your way to writing efficient, optimized code. Remember, understanding these concepts is crucial for any programmer who wants to create scalable, high-performance applications. So, dive in, have fun, and don’t be afraid to make mistakes – they’re just stepping stones to becoming a better coder.
By following these tips and incorporating a bit of humor into your learning process, you’ll find that mastering time and space complexity is not only achievable but also enjoyable. Happy coding!